8  Intro to Models

In this lecture we will learn about modeling data for the first time. After this lesson, you should know what we generally mean by a “model”, what linear regression is and how to interpret the output. But first we need to introduce a new data type: categorical variables.

  1. Categorical variables
  2. Models

Online Resources:

Chapter 7.5 of our textbook introduces categorical variables.

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from numpy.random import default_rng
import statsmodels.api as sm
import statsmodels.formula.api as smf
#!pip install gapminder
from gapminder import gapminder
gapminder.head()
country continent year lifeExp pop gdpPercap
0 Afghanistan Asia 1952 28.801 8425333 779.445314
1 Afghanistan Asia 1957 30.332 9240934 820.853030
2 Afghanistan Asia 1962 31.997 10267083 853.100710
3 Afghanistan Asia 1967 34.020 11537966 836.197138
4 Afghanistan Asia 1972 36.088 13079460 739.981106

Categorical variables

As a motivation, take another look at the gapminder data which contains variables of a mixed type: numeric columns along with string type columns which contain repeated instances of a smaller set of distinct or discrete values which

  1. are not numeric (but could be represented as numbers)
  2. cannot really be ordered
  3. typically take on a finite set of values, or categories.

We refer to these data types as categorical.

We have already seen functions like unique and value_counts, which enable us to extract the distinct values from an array and compute their frequencies.

Boxplots and grouping operations typically use a categorical variable to compute summaries of a numerical variables for each category separately, e.g.

gapminder.boxplot(column = "lifeExp", by="continent",figsize=(5, 2));
plt.title('Life expectancy by continent')
# Remove the default suptitle
plt.suptitle("");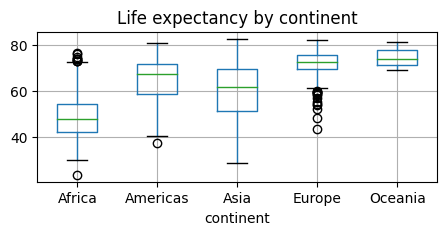

pandas has a special Categorical extension type for holding data that uses the integer-based categorical representation or encoding. This is a popular data compression technique for data with many occurrences of similar values and can provide significantly faster performance with lower memory use, especially for string data.

gapminder.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1704 entries, 0 to 1703
Data columns (total 6 columns):
 #   Column     Non-Null Count  Dtype  
---  ------     --------------  -----  
 0   country    1704 non-null   object 
 1   continent  1704 non-null   object 
 2   year       1704 non-null   int64  
 3   lifeExp    1704 non-null   float64
 4   pop        1704 non-null   int64  
 5   gdpPercap  1704 non-null   float64
dtypes: float64(2), int64(2), object(2)
memory usage: 80.0+ KB
gapminder['country'] = gapminder['country'].astype('category')
gapminder.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1704 entries, 0 to 1703
Data columns (total 6 columns):
 #   Column     Non-Null Count  Dtype   
---  ------     --------------  -----   
 0   country    1704 non-null   category
 1   continent  1704 non-null   object  
 2   year       1704 non-null   int64   
 3   lifeExp    1704 non-null   float64 
 4   pop        1704 non-null   int64   
 5   gdpPercap  1704 non-null   float64 
dtypes: category(1), float64(2), int64(2), object(1)
memory usage: 75.2+ KB

We will come back to the usefulness of this later.

Tables as models

For now let us look at our first “model”:

titanic = sns.load_dataset('titanic')
titanic["class3"] = (titanic["pclass"]==3)
titanic["male"] = (titanic["sex"]=="male")
titanic.head()
survived pclass sex age sibsp parch fare embarked class who adult_male deck embark_town alive alone class3 male
0 0 3 male 22.0 1 0 7.2500 S Third man True NaN Southampton no False True True
1 1 1 female 38.0 1 0 71.2833 C First woman False C Cherbourg yes False False False
2 1 3 female 26.0 0 0 7.9250 S Third woman False NaN Southampton yes True True False
3 1 1 female 35.0 1 0 53.1000 S First woman False C Southampton yes False False False
4 0 3 male 35.0 0 0 8.0500 S Third man True NaN Southampton no True True True 
vals1, cts1 = np.unique(titanic["class3"], return_counts=True)
print(cts1)
print(vals1)
[400 491]
[False  True]
print("The mean survival on the Titanic was", np.mean(titanic.survived))
The mean survival on the Titanic was 0.3838383838383838
ConTbl = pd.crosstab(titanic["sex"], titanic["survived"])
ConTbl
survived 0 1
sex
female 81 233
male 468 109

What are the estimated survival probabilities?

#the good old groupby way:
bySex = titanic.groupby("sex").survived
bySex.mean()
sex
female    0.742038
male      0.188908
Name: survived, dtype: float64
p3D = pd.crosstab([titanic["sex"], titanic["class3"]], titanic["survived"])
p3D
survived 0 1
sex class3
female False 9 161
True 72 72
male False 168 62
True 300 47

What are the estimated survival probabilities?

#the good old groupby way:
bySex = titanic.groupby(["sex", "class3"]).survived
bySex.mean()
sex     class3
female  False     0.947059
        True      0.500000
male    False     0.269565
        True      0.135447
Name: survived, dtype: float64

The above table can be looked at as a model, which is defined as a function which takes inputs x and “spits out” a prediction:

\(y = f(\mathbf{x})\)

In our case, the inputs are \(x_1=\text{sex}\), \(x_2=\text{class3}\), and the output is the estimated survival probability!

It is evident that we could keep adding more input variables and make finer and finer grained predictions.

Linear Models

lsFit = smf.ols('survived ~ sex:class3-1', titanic).fit()
lsFit.summary().tables[1]
coef std err t P>|t| [0.025 0.975]
sex[female]:class3[False] 0.9471 0.029 32.200 0.000 0.889 1.005
sex[male]:class3[False] 0.2696 0.025 10.660 0.000 0.220 0.319
sex[female]:class3[True] 0.5000 0.032 15.646 0.000 0.437 0.563
sex[male]:class3[True] 0.1354 0.021 6.579 0.000 0.095 0.176

Modeling Missing Values

We have already seen how to detect and how to replace missing values. But the latter -until now- was rather crude: we often replaced all values with a “global” average.

Clearly, we can do better than replacing all missing entries in the survived column with the average \(0.38\).

rng = default_rng()

missingRows = rng.integers(0,890,20)
print(missingRows)
#introduce missing values
titanic.iloc[missingRows,0] = np.nan
np.sum(titanic.survived.isna())
[864 299 857 182 808 817 802 295 255 644   1 685 452 463 303 551 517 502
 495 412]
20
predSurv = lsFit.predict()
print( len(predSurv))
predSurv[titanic.survived.isna()]
891
array([0.94705882, 0.13544669, 0.5       , 0.26956522, 0.94705882,
       0.94705882, 0.94705882, 0.26956522, 0.26956522, 0.13544669,
       0.5       , 0.13544669, 0.26956522, 0.5       , 0.26956522,
       0.26956522, 0.26956522, 0.26956522, 0.26956522, 0.26956522])

From categorical to numerical relations

url = "https://drive.google.com/file/d/1UbZy5Ecknpl1GXZBkbhJ_K6GJcIA2Plq/view?usp=share_link" 
url='https://drive.google.com/uc?id=' + url.split('/')[-2]
auto = pd.read_csv(url)
auto.head()
mpg cylinders displacement horsepower weight acceleration year origin name Manufacturer
0 18.0 8 307.0 130 3504 12.0 70 1 chevrolet chevelle malibu chevrolet
1 15.0 8 350.0 165 3693 11.5 70 1 buick skylark 320 buick
2 18.0 8 318.0 150 3436 11.0 70 1 plymouth satellite plymouth
3 16.0 8 304.0 150 3433 12.0 70 1 amc rebel sst amc
4 17.0 8 302.0 140 3449 10.5 70 1 ford torino ford 
plt.figure(figsize=(5,3))
plt.scatter(x=auto["weight"], y=auto["mpg"]);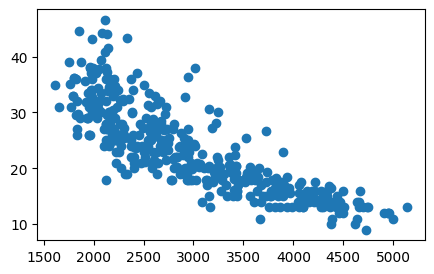

Linear Regression

We can roughly estimate, i.e. “model” this relationship with a straight line:

\[ y = \beta_0 + \beta_1 x \]

plt.figure(figsize=(5,3))
tmp=sns.regplot(x=auto["weight"], y=auto["mpg"], order=1, ci=95, 
                scatter_kws={'color':'b', 's':9}, line_kws={'color':'r'})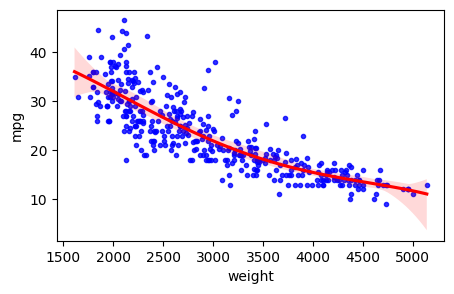

Remind yourself of the definition of the slope of a straight lineSlopeIllustration.png

\[ \beta_1 = \frac{\Delta y}{\Delta x} = \frac{y_2-y_1}{x_2-x_1} \]

est = smf.ols('mpg ~ weight', auto).fit()
est.summary().tables[1]
coef std err t P>|t| [0.025 0.975]
Intercept 46.2165 0.799 57.867 0.000 44.646 47.787
weight -0.0076 0.000 -29.645 0.000 -0.008 -0.007 
np.corrcoef(auto["weight"], auto["mpg"])
array([[ 1.        , -0.83224421],
       [-0.83224421,  1.        ]])

Further Reading: